Co je analytická geometrie?
Co je analytická geometrie?
Analytická geometrie je odvětví algebry, které se používá k modelování geometrických objektů – nejzákladnější z nich jsou body, (přímky) a kružnice. Analytická geometrie je velkým vynálezem Descarta a Fermata.
V rovinné analytické geometrii jsou body definovány jako uspořádané dvojice čísel, řekněme (x, y), zatímco přímky jsou zase definovány jako množiny bodů, které splňují lineární rovnice, viz vynikající výklady D. Pedoeho nebo D. Brannana a dalších. Z hlediska analytické geometrie jsou geometrické axiomy odvozené věty. Například pro libovolné dva různé body (x1, y1) a (x2, y2) existuje jediná přímka ax + by + c = 0, která těmito body prochází. Její koeficienty a, b, c lze zjistit (až na konstantní činitel) z lineární soustavy dvou rovnic
| ax1 + by1 + c = 0 ax2 + by2 + c = 0, |
nebo přímo z determinantové rovnice
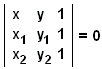 |
Žádná axiomatická teorie však nesmí uniknout použití neurčitých prvků. V teorii množin, která je základem velké části matematiky a zejména analytické geometrie, zůstává nejzákladnější pojem množiny neurčitý.
Geometrie trojrozměrného prostoru je modelována trojicemi čísel (x, y, z) a 3D lineární rovnice ax + by + cz + d = 0 definuje rovinu. Obecně analytická geometrie poskytuje vhodný nástroj pro práci ve vyšších dimenzích.
V rámci analytické geometrie lze modelovat (a modeluje se) i neeuklidovské geometrie. Například v rovinné projektivní geometrii je bod trojice homogenních souřadnic (x, y, z), ne všechny 0, taková, že
| (tx, ty, tz) = (x, y, z), |
pro všechna t ≠ 0, zatímco přímka je popsána homogenní rovnicí
| ax + bx + cz = 0. |
V analytické geometrii jsou kuželosečky definovány rovnicemi druhého stupně:
| ax² + bxy + cy² + dx + ey + f = 0. |
Ta část analytické geometrie, která se zabývá především lineárními rovnicemi, se nazývá lineární algebra.
Kartézská analytická geometrie je geometrie, v níž jsou osy x = 0 a y = 0 kolmé.
Složky n-tice x = (x1, …, xn) se nazývají její souřadnice. Je-li n = 2 nebo n = 3, nazývá se první souřadnice abscisou a druhá ordinátou.
- D. A. Brannan, M. F. Esplen, J. J. Gray, Geometry, Cambridge University Press, 2002
- D. Pedoe, Geometry: A Comprehensive Course, Dover, 1988
|Kontakt|||Přední strana||Obsah||Geometrie||Nahoru|
Copyright © 1996-2018 Alexander Bogomolny
Leave a Reply