Bilineární filtrování a bilineární interpolace

Podívejte se na obrázek níže. Dokážete vypočítat hodnoty v bodech A,B a C?“

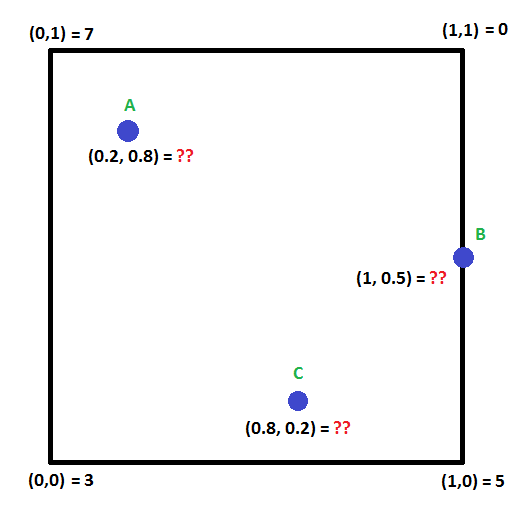
K tomu existuje technika zvaná bilineární interpolace, která rozšiřuje myšlenku lineární interpolace do dvou rozměrů.

Pro výpočet bilineární interpolace stačí provést lineární interpolaci na jedné ose a pak na druhé.

Podívejte se na tyto příklady:

Bod A
Bod A má souřadnici (0,2,0,8). Začněme s osou X.

Nejprve provedeme interpolaci přes vrchol čtverce na ose X.

Připravte si obrázek. To znamená, že musíme projít 0,2 (20 %) cesty ze 7 na 0. Těchto 0,2 je naše souřadnice na ose X. To vypočítáme takto:
7 + (0-7) * 0,2 = 5,6

Dále provedeme interpolaci přes spodní část čtverce na ose X. Takže podobně jako výše půjdeme 0,2 (20 %) z cesty od 3 do 5. Pro výpočet to uděláme takto:
3 + (5-3) * 0,2 = 3,4

Teď, když jsme interpolovali přes osu X, musíme interpolovat přes osu Y. V tomto případě je třeba provést interpolaci přes osu X. Nyní projdeme 0,8 (80 %) cesty od naší spodní hodnoty (hodnota Y = 0) k naší horní hodnotě (hodnota Y = 1). Spodní hodnota je spodní interpolace, kterou jsme provedli (3,4), a horní hodnota je horní interpolace, kterou jsme provedli (5,6).

Potřebujeme tedy projít 0,8 (80 %) cesty od hodnoty 3,4 k hodnotě 5,6. To znamená, že musíme projít 0,8 (80 %) cesty. To vypočítáme takto:
3,4 + (5,6 – 3,4) * 0,8 = 5,16

Takže hodnota v bodě A je 5,16. To znamená, že hodnota v bodě A je 5,16. Následující obrázek by měl pomoci vizuálně vysvětlit postup, kterým jsme prošli.

Bod B

Bod B má souřadnice (1,0,0,5).

Znovu začneme s interpolací na ose X (i když byste klidně mohli začít nejprve s Y, pokud byste chtěli! Skončili byste se stejným výsledkem).

Provádíme-li interpolaci osy X přes vrchol, musíme projít 1,0 (100 %) cesty ze 7 na 0. Určitě tušíte, jaká je odpověď, ale zde je vypočtena:
7 + (0-7) * 1,0 = 0

Podobně proveďme interpolaci osy X přes spodek. Potřebujeme projít 1,0 (100 %) cesty od 3 do 5.
3 + (5-3) * 1,0 = 5

Následuje interpolace osy Y. V tomto případě se jedná o interpolaci osy X, kterou provedeme na ose X. Potřebujeme jít 0,5 (50 %) cesty z 5 na 0.
5 + (0-5) * 0,5 = 2,5

Tady to máme, hodnota v bodě B je 2,5.

. To by mělo dávat smysl i při pohledu na diagram. Je to v podstatě 1d lineární interpolace mezi hodnotami 5 a 0 a je v polovině cesty mezi nimi, takže intuitivně by měla dávat smysl odpověď 2,5.

Bod C

Bod C má souřadnici (0,8,0,2).

Znovu provedeme interpolaci osy X přes horní část rámečku. Potřebujeme projít 0,8 (80 %) cesty ze 7 na 0.
7 + (0-7) * 0,8 = 1,4

Poté musíme provést interpolaci osy X přes spodní část boxu. Potřebujeme projít 0,8 (80 %) cesty z 3 na 5.
3 + (5-3) * 0,8 = 4,6

Nakonec provedeme interpolaci osy y. V tomto případě je třeba provést interpolaci osy x. Musíme jít 0,2 (20 %) od 4,6 do 1,4.
4,6 + (1,4-4,6) * 0,2 = 3,96

Hodnota bodu C je 3.
.96

Bilineární filtrování

Bilineární interpolace je sice užitečná, pokud máte mřížku dat, v rámci které chcete interpolovat hodnoty (například výškové pole, které představuje terén?!), ale kde při vývoji her opravdu zazáří, je bilineární filtrování textur.

V podstatě jde o to, že když máte souřadnici textury, která se dokonale neshoduje se středem pixelu v textuře (protože je tam zbytek), použije se zlomková část souřadnice v rámci tohoto pixelu k provedení bilineární interpolace mezi 4 zúčastněnými pixely, aby se získala výsledná barva pixelu. Provádí bilineární interpolaci pro každý z kanálů:

Konečný výsledek je docela dobrý! Podívejte se na obrázek níže a uvidíte jej v akci na textuře, kterou jsme příliš přiblížili. Na levé straně je použito bilineární filtrování, zatímco na pravé straně ne a zobrazuje se pouze nejbližší pixel.

V důsledku toho musí bilineární filtrování textur provést čtení 4 pixelů, aby bylo možné mezi nimi interpolovat, namísto čtení jednoho pixelu jako při vzorkování nejbližšího pixelu. Více čtení pixelů = větší režie a ne tak levné (výpočetně) použití.

Odkazy

Pro některé lidi, kteří to čtou, jsou tyto informace docela základní a možná se divíte, proč jsem se o tom obtěžoval psát. Podívejte se na další příspěvek, kde najdete něco poněkud bizarního ohledně bilineární filtrace. Tohle bylo potřeba jako odrazový můstek k další věci, kterou vám chci ukázat 😛

Wikipedie: Lineární interpolace

Wikipedia:

Wikipedia: Bilineární interpolace

Wikipedia:

Podívejte se na tyto odkazy, kde najdete hlubší informace o některých nedostatcích (a některých řešeních) hardwarového bilineárního vzorkování:
iq: hardwarová interpolace
iq: vylepšená interpolace textur

.