Algoritmus a schéma Fibonacciho řady

Fibonacciho řada je definována jako posloupnost čísel, v níž první dvě čísla jsou 1 a 1 nebo 0 a 1 v závislosti na zvoleném počátečním bodě posloupnosti a každé další číslo je součtem předchozích dvou. V této řadě je tedy n-tý člen součtem (n-1)-ho a (n-2)-ho členu. V tomto tutoriálu probereme jednoduchý algoritmus a vývojový diagram Fibonacciho řady spolu se stručným úvodem do Fibonacciho řady a některými jejími důležitými vlastnostmi.

Než vás provedeme zdrojovým kódem v Algoritmu a vývojovém diagramu Fibonacciho řady, dovolte mi nejprve vysvětlit několik věcí o této úžasné řadě, její matematické odvození a vlastnosti. Více informací o Fibonacciho řadě si můžete přečíst v našem dřívějším příspěvku – Program v jazyce C pro Fibonacciho řadu, a zde jsou další odkazy, které můžete sledovat – Odkaz 1. Odkaz 2.

Jak generovat Fibonacciho řadu?

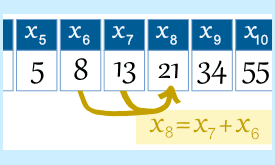
Matematicky lze n-tý člen Fibonacciho řady znázornit jako:

tn = tn-1 + tn-2

Fibonacciho čísla do určitého členu lze znázornit jako: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144….. nebo 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144….

Tato hlavní vlastnost se používá v algoritmu a schématu pro fibonacciho řady. Řada začíná buď číslem 0, nebo 1 a součet každého následujícího členu je součtem předchozích dvou členů takto:

První člen = 0
Druhý člen = 1
Třetí člen = První + Druhý = 0+1 =1
Čtvrtý člen = Druhý + Třetí. =1+1 = 2
Pátý termín = třetí + čtvrtý = 2+1 = 3
Šestý termín = čtvrtý + pátý = 3+2 = 5
Sedmý termín = pátý + šestý = 3+5 = 8
Osmý termín = šestý + sedmý = 5+8 = 13 … a tak dále do nekonečna!

Algoritmus Fibonacciho řady:

• Start
• Deklarovat proměnné i, a,b , ukázat
• Inicializovat proměnné, a=0, b=1, a show =0
• Zadejte počet členů Fibonacciho řady, které se mají vytisknout
• Vytiskněte první dva členy řady
• V následujících krocích použijte smyčku
  -> show=a+b
  -> a=b
  -> b=show
  -> zvyšte hodnotu i vždy o 1
  -> vytiskněte hodnotu show
• Konec

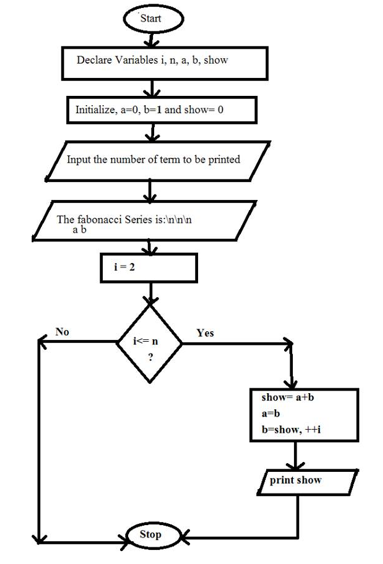
Vývojový diagram Fibonacciho řady:

Také viz,
Program Fibonacciho řady v jazyce C
Algoritmus/vývojový diagram Pascalova trojúhelníku
Algoritmus/vývojový diagram Hanojské věže