9.5 – Identifikace vlivných datových bodů

V této části se naučíme následující dvě míry pro identifikaci vlivných datových bodů:

• Difference in Fits (DFFITS)
• Cookovy vzdálenosti

Základní myšlenka každé z těchto měr je stejná, a to vymazat pozorování po jednom a pokaždé znovu fitovat regresní model na zbývajících n-1 pozorování. Poté porovnáme výsledky s použitím všech n pozorování s výsledky s odstraněným i-tým pozorováním, abychom zjistili, jak velký vliv má toto pozorování na analýzu. Při takto provedené analýze jsme schopni posoudit potenciální vliv každého datového bodu na regresní analýzu.

Rozdíl ve shodách (DFFITS)

Rozdíl ve shodách pro pozorování i, označený jako DFFITSi, je definován jako:

\

Jak vidíte, čitatel měří rozdíl v předpovězených odpovědích získaných při zahrnutí a vyloučení i-tého datového bodu z analýzy. Ve jmenovateli je odhadnutá směrodatná odchylka rozdílu v předpovídaných odpovědích. Rozdíl ve shodách tedy kvantifikuje počet směrodatných odchylek, o které se změní fitovaná hodnota při vynechání i-tého datového bodu.

Pozorování je považováno za vlivné, pokud je absolutní hodnota jeho hodnoty DFFITS větší než:

\

kde jako vždy platí, že n = počet pozorování a k = počet predikčních členů (tj. počet regresních parametrů bez interceptu). Je důležité mít na paměti, že se nejedná o pevně dané pravidlo, ale spíše pouze o vodítko! Není těžké najít různé autory, kteří používají mírně odlišné vodítko. Proto často dávám přednost mnohem subjektivnějšímu vodítku, například že datový bod je považován za vlivný, pokud absolutní hodnota jeho hodnoty DFFITS vyčnívá z ostatních hodnot DFFITS jako bolavý palec. Samozřejmě se jedná o kvalitativní úsudek, možná takový, jaký by měl být, protože odlehlé hodnoty jsou ze své podstaty subjektivní veličiny.

Příklad č. 2 (opět). Podívejme se na míru rozdílu ve shodách pro tento soubor dat (influence2.txt):

Regresí y na x a požadavkem na rozdíl ve shodách získáme následující softwarový výstup:

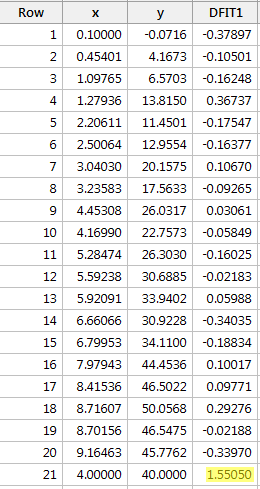
Podle výše definovaného objektivního vodítka považujeme datový bod za vlivný, pokud je absolutní hodnota jeho hodnoty DFFITS větší než:

\

Pouze jeden datový bod – červený – má hodnotu DFFITS, jejíž absolutní hodnota (1.55050) je větší než 0,82. Proto bychom na základě tohoto pokynu považovali červený datový bod za vlivný.

Příklad č. 3 (opět). Podívejme se na míru rozdílu ve shodách pro tento soubor dat (influence3.txt):

Regresí y na x a požadavkem na rozdíl ve shodách získáme následující softwarový výstup:

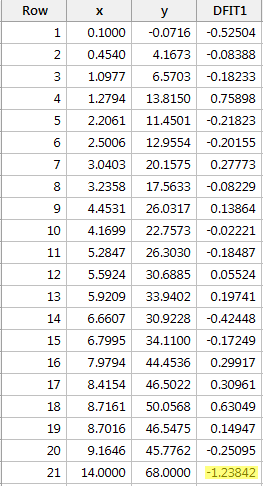
Podle výše definovaného objektivního vodítka považujeme datový bod za vlivný, pokud je absolutní hodnota jeho hodnoty DFFITS větší než:

\

Pouze jeden datový bod – červený – má hodnotu DFFITS, jejíž absolutní hodnota (1.23841) je větší než 0,82. Na základě této směrnice bychom tedy červený datový bod považovali za vlivný.

Když jsme na začátku této lekce studovali tento soubor dat, rozhodli jsme se, že červený datový bod nemá na regresní analýzu až takový vliv. Přesto zde rozdíl v míře shody naznačuje, že vlivný skutečně je. Co se zde děje? Vše spočívá v tom, že si uvědomíme, že všechna opatření v této lekci jsou pouze nástroje, které označují potenciálně vlivné datové body pro datového analytika. Nakonec by měl analytik analyzovat soubor dat dvakrát – jednou s označenými datovými body a jednou bez nich. Pokud tyto datové body významně mění výsledek regresní analýzy, pak by měl výzkumník uvést výsledky obou analýz.

Mimochodem, pokud v tomto příkladu zde použijeme subjektivnější vodítko, zda absolutní hodnota hodnoty DFFITS vyčnívá jako bolavý palec, pravděpodobně nebudeme červený datový bod považovat za vlivný. Koneckonců další největší hodnota DFFITS (v absolutní hodnotě) je 0,75898. Tato hodnota DFFITS se od hodnoty DFFITS našeho „vlivného“ datového bodu příliš neliší.

Příklad č. 4 (opět). Podívejme se na míru rozdílu ve shodách pro tento soubor dat (influence4.txt):

Regresí y na x a požadavkem na rozdíl ve shodách získáme následující softwarový výstup:

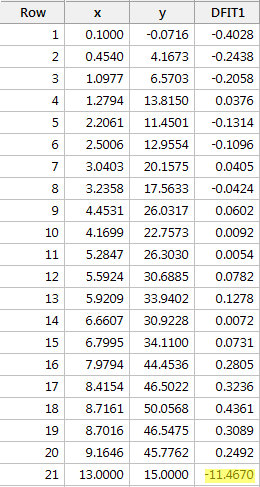
Podle výše definovaného objektivního vodítka opět považujeme datový bod za vlivný, pokud je absolutní hodnota jeho hodnoty DFFITS větší než:

\

Co myslíte? Vyčnívá některá z hodnot DFFITS jako bolavý palec? Errr – hodnota DFFITS červeného datového bodu (-11,4670 ) má určitě jinou velikost než všechny ostatní. V tomto případě by nemělo být pochyb o tom, že červený datový bod je vlivný!

Cookova vzdálenost

Jen na skok, Cookova míra vzdálenosti, označovaná Di, je definována jako:

\.\]

Vypadá to trochu nepřehledně, ale hlavní věc, kterou je třeba si uvědomit, je, že Cookova Di závisí jak na reziduu, ei (v prvním členu), tak na páce, hii (ve druhém členu). To znamená, že při výpočtu Cookovy vzdálenosti hraje roli jak hodnota x, tak hodnota y datového bodu.

Zkrátka:

• Di přímo shrnuje, jak moc se změní všechny fitované hodnoty, když se odstraní i-té pozorování.
• Datový bod, který má velké Di, znamená, že tento datový bod silně ovlivňuje fitované hodnoty.

Prozkoumejme, co přesně toto první tvrzení znamená v kontextu některých našich příkladů.

Příklad č. 1 (znovu). Možná si vzpomenete, že graf těchto dat (influence1.txt) naznačuje, že pro tento příklad neexistují žádné odlehlé ani vlivné datové body:

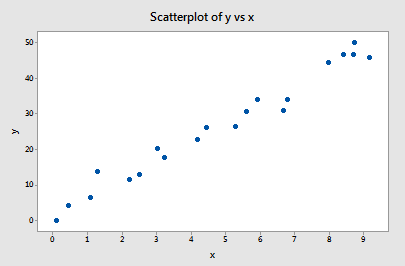
Pokud regresujeme y na x s použitím všech n = 20 datových bodů, zjistíme, že odhadovaný koeficient intercepce b0 = 1,732 a odhadovaný koeficient sklonu b1 = 5,117. To znamená, že odhadovaný koeficient intercepce b0 = 1,732 a odhadovaný koeficient sklonu b1 = 5,117. To znamená, že odhadovaný koeficient sklonu b1 = 5,117. Pokud ze souboru dat odstraníme první datový bod a regresi y na x provedeme pomocí zbývajících n = 19 datových bodů, zjistíme, že odhadovaný koeficient intercepce b0 = 1,732 a odhadovaný koeficient sklonu b1 = 5,1169. Jak bychom doufali a očekávali, odhady se po odstranění jednoho datového bodu příliš nezmění. Pokračujeme-li v tomto procesu postupného odstraňování každého datového bodu a vykreslíme-li výsledné odhady sklonů (b1) versus odhady průsečíků (b0), získáme:

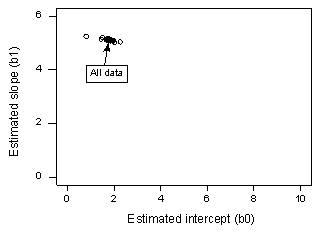
Plný černý bod představuje odhadované koeficienty na základě všech n = 20 datových bodů. Otevřené kruhy představují jednotlivé odhadované koeficienty získané při postupném vymazávání každého datového bodu. Jak je vidět, odhadované koeficienty jsou všechny pohromadě bez ohledu na to, který datový bod, pokud vůbec nějaký, je odstraněn. To naznačuje, že žádný datový bod nepatřičně neovlivňuje odhadovanou regresní funkci a následně ani přizpůsobené hodnoty. V tomto případě bychom očekávali, že všechny Cookovy míry vzdálenosti Di budou malé.

Příklad č. 4 (opět). Možná si vzpomenete, že graf těchto dat (influence4.txt) naznačuje, že jeden datový bod je pro tento příklad vlivný a odlehlý:

Pokud regresujeme y na x s použitím všech n = 21 datových bodů, zjistíme, že odhadovaný koeficient intercepce b0 = 8,51 a odhadovaný koeficient sklonu b1 = 3,32. V případě, že se v tomto případě jedná o odlehlý bod, je možné, že se jedná o odlehlý bod. Pokud ze souboru dat odstraníme červený datový bod a regresi y na x provedeme pomocí zbývajících n = 20 datových bodů, zjistíme, že odhadovaný koeficient intercepce b0 = 1,732 a odhadovaný koeficient sklonu b1 = 5,1169. Páni – odhady se po odstranění jednoho datového bodu podstatně změní. Pokračujeme-li v tomto procesu postupného odstraňování každého datového bodu a vykreslíme-li výsledné odhady sklonů (b1) versus odhady průsečíků (b0), získáme:

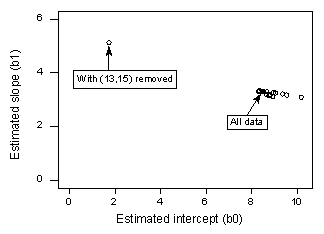
Znovu platí, že plný černý bod představuje odhadované koeficienty na základě všech n = 21 datových bodů. Otevřené kruhy představují jednotlivé odhadované koeficienty získané při postupném vymazávání každého datového bodu. Jak vidíte, s výjimkou červeného datového bodu (x = 13, y = 15) jsou všechny odhadované koeficienty pohromadě bez ohledu na to, který datový bod, pokud vůbec nějaký, je odstraněn. To naznačuje, že červený datový bod je jediným datovým bodem, který nepatřičně ovlivňuje odhadovanou regresní funkci a následně i fitované hodnoty. V tomto případě bychom očekávali, že Cookova míra vzdálenosti, Di, pro červený datový bod bude velká a Cookovy míry vzdálenosti, Di, pro ostatní datové body budou malé.

Použití Cookových měr vzdálenosti. Krása výše uvedených příkladů spočívá v možnosti vidět, o co jde, pomocí jednoduchých grafů. V případě vícenásobné regrese se bohužel na jednoduché grafy spolehnout nemůžeme. Místo toho se musíme spolehnout na pokyny pro rozhodování, kdy je Cookova míra vzdálenosti dostatečně velká na to, aby bylo oprávněné považovat datový bod za vlivný.

Níže jsou uvedeny běžně používané pokyny:

• Pokud je Di větší než 0,5, pak i-tý datový bod stojí za další zkoumání, protože může být vlivný.
• Pokud je Di větší než 1, pak je dost pravděpodobné, že i-tý datový bod je vlivný.
• Nebo pokud Di vyčnívá jako bolavý palec z ostatních hodnot Di, je téměř jistě vlivný.

Příklad č. 2 (opět). Podívejme se na Cookovu míru vzdálenosti pro tento soubor dat (influence2.txt):

Regresí y na x a vyžádáním Cookových měr vzdálenosti získáme následující softwarový výstup:

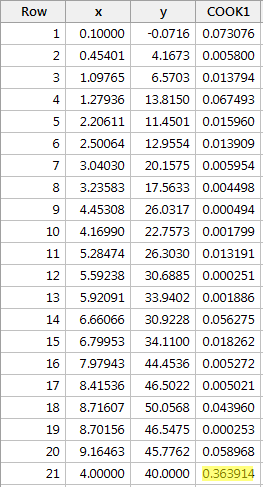
Ve srovnání s ostatními Cookovými mírami vzdálenosti trochu vyčnívá Cookova míra vzdálenosti pro červený datový bod (0,363914). Přesto je Cookova míra vzdálenosti pro červený datový bod menší než 0,5. Proto bychom na základě Cookovy míry vzdálenosti červený datový bod neklasifikovali jako vlivný.

Příklad č. 3 (opět). Podívejme se na Cookovu míru vzdálenosti pro tento soubor dat (influence3.txt):

Regresí y na x a vyžádáním Cookovy míry vzdálenosti získáme následující softwarový výstup:

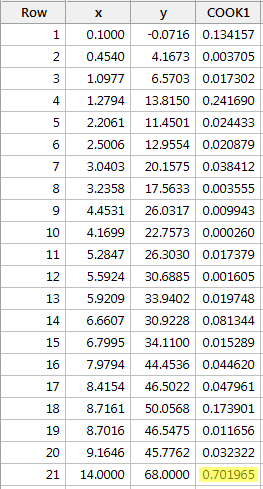
Cookova míra vzdálenosti pro červený datový bod (0,701965) trochu vyčnívá ve srovnání s ostatními Cookovými mírami vzdálenosti. Přesto je Cookova míra vzdálenosti pro červený datový bod větší než 0,5, ale menší než 1. Proto bychom na základě Cookovy míry vzdálenosti možná dále zkoumali, ale ne nutně klasifikovali červený datový bod jako vlivný.

Příklad č. 4 (opět). Zkontrolujme Cookovu míru vzdálenosti pro tuto sadu dat (influence4.txt):

Regresí y na x a vyžádáním Cookovy míry vzdálenosti získáme následující softwarový výstup:

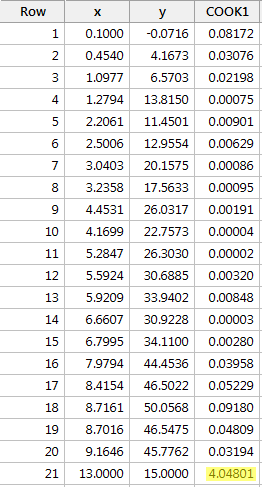
V tomto případě Cookova míra vzdálenosti pro červený datový bod (4. Vliv4.txt) ukazuje, že Cookova míra vzdálenosti pro červený datový bod (4. Vliv4.txt) je v rozporu s Cookovou mírou vzdálenosti.04801) ve srovnání s ostatními Cookovými mírami vzdálenosti výrazně vyniká. Navíc Cookova míra vzdálenosti pro červený datový bod je větší než 1. Proto bychom na základě Cookovy míry vzdálenosti – a není to překvapivé – klasifikovali červený datový bod jako vlivný.

Alternativní metodou interpretace Cookovy míry vzdálenosti, která se někdy používá, je vztáhnout tuto míru k rozdělení F(k+1, n-k-1) a zjistit odpovídající hodnotu percentilu. Pokud je tento percentil menší než přibližně 10 nebo 20 procent, pak má daný případ jen malý zjevný vliv na fitované hodnoty. Na druhou stranu, pokud se blíží 50 procentům nebo je dokonce vyšší, pak má případ významný vliv. (Cokoli „mezi tím“ je nejednoznačnější.)