Část 14 : Tečkový a Hadamardův součin

Kromě dříve probíraného násobení matic lze vektory násobit ještě dvěma způsoby : Tečkový součin a Hadamardův součin. Výsledky získané oběma metodami se liší.

Prvky odpovídající stejnému řádku a sloupci se vynásobí dohromady a součin se sečte tak, že výsledkem je skalár.

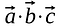
Na rozdíl od maticového násobení není výsledkem tečkového součinu jiný vektor nebo matice, je to skalár.

Při tečkovém součinu nezáleží na pořadí vektorů, jen počet prvků v obou vektorech musí být stejný.

Geometrický vzorec pro tečkový součin je

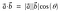
Tečkový součin se také nazývá vnitřní součin nebo skalární součin.

Projekce vektoru

Předpokládáme, že máme dva vektory c a d, které svírají úhel phi(Ф).

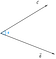
Nyní, projekci vektoru c na vektor d lze znázornit jako

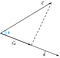
Z obrázku můžeme vyvodit, že projekce je rovna vodorovné složce vektoru c vzhledem k úhlu phi(Ф).

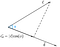
Toto promítání se nazývá skalární.Abychom zjistili vektorový průmět vektoru c na vektor d, musíme skalární průmět vynásobit jednotkovým vektorem d.

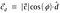
Podložení hodnoty jednotkového vektoru d.

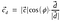
Takto, bodový součin lze také reprezentovat jako

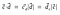
Projekce mají široké využití v lineární algebře a strojovém učení (Support Vector Machine(SVM) je algoritmus strojového učení, používaný pro klasifikaci dat).

Hadamardův součin (násobení po prvcích)

Hadamardův součin dvou vektorů je velmi podobný maticovému sčítání, prvky odpovídající stejným řádkům a sloupcům daných vektorů/matic se vynásobí dohromady a vytvoří nový vektor/matici.

Je pojmenován po francouzském matematikovi Jacquesu Hadamardovi.

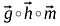
Pořadí matic/vektorů, které se mají násobit, by mělo být stejné a výsledná matice bude mít také stejné pořadí.

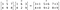
Hadamardův součin se používá v technikách komprese obrazu, například JPEG. Je také známý jako Schurův součin podle německého matematika Issaie Schura.

Hadamardův součin se používá v buňkách LSTM (Long Short-Term Memory) rekurentních neuronových sítí (RNN).

.