Úvod do dekonvoluce

Dekonvoluce je výpočetně náročná technika zpracování obrazu, která se stále více využívá ke zlepšení kontrastu a rozlišení digitálních snímků pořízených v mikroskopu. Její základy jsou založeny na souboru metod, které mají odstranit nebo zvrátit rozmazání přítomné v obrazech z mikroskopu vyvolané omezenou aperturou objektivu.

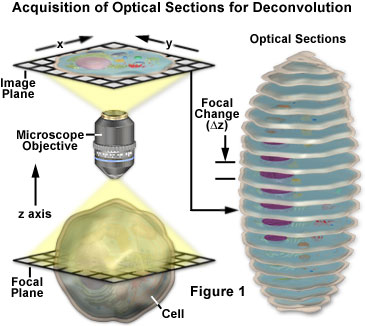
Téměř každý obraz získaný digitálním fluorescenčním mikroskopem lze dekonvolvovat a vyvíjí se několik nových aplikací, které používají techniky dekonvoluce na obrazy v procházejícím světle získané při různých strategiích zvyšování kontrastu. Mezi nejvhodnější předměty pro vylepšení pomocí dekonvoluce patří trojrozměrné montáže sestavené z řady optických řezů.

Základní koncepty týkající se pořizování obrazů řady Z pro dekonvoluční analýzu jsou uvedeny pomocí schématu na obrázku 1. Zaznamená se řada snímků vzorku, z nichž každý je od sebe mírně posunutý podél osy z. Výsledkem této změny ohniskové roviny je mírně odlišný obraz s jemnými změnami způsobenými rozostřeným světlem přicházejícím shora a zespodu aktuální z-roviny. Během dekonvoluční analýzy se analyzuje celá řada z, aby se vytvořil jasnější soubor dat s vyšším rozlišením, který není zkreslený rozostřenou fluorescencí.

Dekonvoluce se často navrhuje jako dobrá alternativa ke konfokálnímu mikroskopu, protože obě techniky se snaží minimalizovat vliv rozostřené fluorescence na výsledný obraz. To není tak docela pravda, protože snímky pořízené pomocí dírkové clony v konfokálním mikroskopu těží ze zpracování dekonvoluce. Konfokální mikroskopie zabraňuje detekci rozostřeného světla tím, že mezi objektiv a detektor umístí dírkovou clonu, kterou mohou procházet pouze rozostřené světelné paprsky. Naproti tomu širokoúhlé mikroskopy umožňují průchod rozostřeného světla přímo k detektoru. Na výsledné snímky se pak použije dekonvoluce, aby se rozostřené světlo buď odečetlo, nebo se přiřadilo zpět ke svému zdroji. Konfokální mikroskopie je zvláště vhodná pro zkoumání silných vzorků, jako jsou embrya nebo tkáně, zatímco dekonvoluční zpracování širokého pole se osvědčilo jako účinný nástroj pro zobrazování vzorků vyžadujících extrémně nízké hladiny osvětlení. Tyto nástroje lze dokonce kombinovat za účelem snížení šumu v obrazech pořízených konfokálním mikroskopem. Většina dekonvolučních experimentů uváděných v literatuře se však týká obrazů zaznamenaných na standardním fluorescenčním mikroskopu se širokým polem.

Zdroje degradace obrazu

Degradaci obrazu lze rozdělit do čtyř nezávislých zdrojů: šum, rozptyl, oslnění a rozmazání. Na obrázku 2 jsou uvedeny příklady vizuálního dopadu každého z nich na stejný obraz.

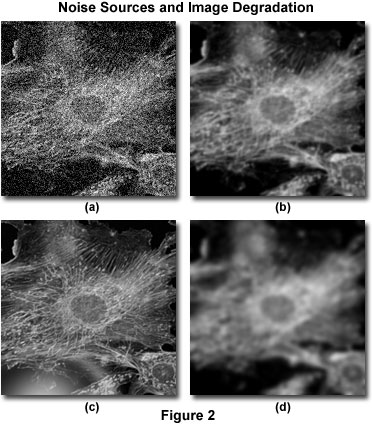
Šum lze popsat jako kvazi-náhodné rozrušení detailů v obraze, které (ve své nejzávažnější podobě) má vzhled bílého šumu nebo šumu typu sůl a pepř, podobně jako je to vidět u televizního vysílání při špatném příjmu (obrázek 2(a)). Tento typ šumu se označuje jako „kvazi-náhodný“, protože jeho statistické rozložení lze předpovědět, pokud je známa mechanika zdroje. V digitální mikroskopii je hlavním zdrojem šumu buď samotný signál (často označovaný jako šum fotonového výstřelu), nebo digitální zobrazovací systém. Mechaniku obou zdrojů šumu známe, a proto je známo i statistické rozdělení šumu. Šum závislý na signálu lze charakterizovat Poissonovým rozdělením, zatímco šum vznikající v zobrazovacím systému se často řídí Gaussovým rozdělením. Protože zdroj a rozložení běžného šumu v digitálních snímcích jsou tak dobře známy, lze jej snadno odstranit použitím vhodných obrazových filtrů, které jsou obvykle součástí většiny dekonvolučních softwarových balíků jako volitelná rutina „předzpracování“.

Rozptyl se obvykle označuje jako náhodné rušení světla vyvolané změnami indexu lomu v celém vzorku. Čistým účinkem rozptylu je skutečně náhodné rozrušení detailů obrazu, jak se projevuje na obrázku 2b). Ačkoli nebyla vyvinuta žádná zcela uspokojivá metoda pro předpověď rozptylu v daném vzorku, bylo prokázáno, že stupeň rozptylu je velmi závislý na tloušťce vzorku a optických vlastnostech vzorku a okolních vkládacích materiálů. Rozptyl se zvyšuje jak s tloušťkou vzorku, tak s heterogenitou indexu lomu, který představují vnitřní složky ve vzorku.

Podobně jako rozptyl je oslnění náhodným narušením světla, k němuž však dochází spíše v optických prvcích (čočkách, filtrech, hranolech atd.) mikroskopu než ve vzorku. Úroveň oslnění v moderním mikroskopu byla minimalizována použitím objektivů a filtrů s antireflexními vrstvami a zdokonalením technik tvarování objektivů, optických tmelů a složení skla. Efekt nekontrolovaného oslnění ilustruje obrázek 2(c).

Rozmazání je popsáno nenáhodným rozptylem světla, ke kterému dochází při průchodu optickou dráhou zobrazovacího systému (obrázek 2(d)). Nejvýznamnějším zdrojem rozmazání je difrakce a obraz, jehož rozlišení je omezeno pouze rozmazáním, se považuje za difrakčně omezený. To představuje vnitřní limit každého zobrazovacího systému a je určujícím faktorem při posuzování limitu rozlišení optického systému. Naštěstí jsou k dispozici sofistikované modely rozmazání v optickém mikroskopu, které lze využít k určení zdroje rozostřených fotonů. To je základem dekonvoluce. Vzhledem k jeho zásadnímu významu pro dekonvoluci bude teoretický model rozmazání mnohem podrobněji diskutován v dalších částech této kapitoly. Je však třeba zdůraznit, že všechny zobrazovací systémy produkují rozmazání nezávisle na jiných formách degradace obrazu vyvolaných vzorkem nebo doprovodnou přístrojovou elektronikou. Právě tato nezávislost optického rozmazání na ostatních typech degradace umožňuje možnost odstranění rozmazání pomocí dekonvolučních technik.

Interakce světla s hmotou je primárním fyzikálním původem rozptylu, oslnění a rozmazání. Složení a uspořádání molekul v daném materiálu (ať už se jedná o sklo, vodu nebo bílkoviny) však propůjčuje každému materiálu jeho vlastní specifický soubor optických vlastností. Pro účely dekonvoluce rozlišují rozptyl, oslnění a rozmazání místa, kde se vyskytují, a možnost vytvoření matematického modelu pro tyto jevy. Protože rozptyl je lokalizovaný, nepravidelný jev vyskytující se ve vzorku, ukázalo se, že je obtížné jej modelovat. Naproti tomu rozmazání je funkcí optického systému mikroskopu (hlavně objektivu), a proto jej lze modelovat relativně jednoduše. Takový model umožňuje zvrátit proces rozmazání matematicky a dekonvoluce využívá tento model ke zvrácení nebo odstranění rozmazání.

Funkce bodového rozptylu

Model rozmazání, který se vyvinul v teoretické optice, je založen na konceptu trojrozměrné funkce bodového rozptylu (PSF). Tento koncept má pro dekonvoluci zásadní význam a měl by být jasně pochopen, abychom se vyhnuli zobrazovacím artefaktům. Funkce bodového rozptylu vychází z nekonečně malého bodového zdroje světla pocházejícího z prostoru vzorku (objektu). Protože zobrazovací systém mikroskopu zachytí pouze zlomek světla vyzařovaného tímto bodem, nemůže světlo zaostřit do dokonalého trojrozměrného obrazu bodu. Místo toho se bod jeví rozšířený a rozprostřený do trojrozměrného difrakčního obrazce. Funkce rozptylu bodu je tedy formálně definována jako trojrozměrný difrakční obrazec generovaný ideálním bodovým zdrojem světla.

V závislosti na použitém režimu zobrazování (širokoúhlé pole, konfokální, procházející světlo) má funkce rozptylu bodu jiný a jedinečný tvar a obrys. V případě fluorescenčního mikroskopu se širokým polem se tvar funkce rozptylu bodu podobá podlouhlému „fotbalovému míči“ světla obklopenému zábleskem rozšiřujících se prstenců. Pro popis funkce bodového rozptylu ve třech rozměrech se běžně používá souřadnicový systém tří os (x, y a z), kde × a y jsou rovnoběžné s ohniskovou rovinou vzorku a z je rovnoběžné s optickou osou mikroskopu. V tomto případě se funkce rozprostření bodu jeví jako soubor soustředných kroužků v rovině x-y a připomíná přesýpací hodiny v rovinách x-z a y-z (jak je znázorněno na obrázku 3). Řez x-y středem funkce rozprostření bodu v širokém poli odhaluje sadu soustředných prstenců: takzvaný Airyho disk, na který se běžně odkazuje v textech o klasické optické mikroskopii.

Dvě x-z projekce funkce rozprostření bodu zobrazující různé stupně sférické aberace jsou uvedeny na obrázku 3. Optická osa je rovnoběžná se svislou osou obrazu. Funkce rozprostření bodu vlevo vykazuje minimální sférickou aberaci, zatímco funkce vpravo vykazuje značný stupeň aberace. Všimněte si, že axiální asymetrie a rozšíření centrálního uzlu podél optické osy na snímku vpravo vede ke zhoršení axiálního rozlišení a rozmazání signálu. Teoreticky je velikost funkce bodového rozptylu nekonečná a celková součtová intenzita světla v rovinách vzdálených od ohniska je rovna součtové intenzitě v ohnisku. Intenzita světla však rychle klesá a nakonec se stává nerozlišitelnou od šumu. V nezkreslené funkci rozptylu bodu zaznamenané pomocí olejového imerzního objektivu s vysokou numerickou aperturou (1,40) se světlo zabírající 0,2 čtverečního mikrometru v rovině zaostření rozprostře na 90násobek této plochy v rovině 1 mikrometru nad a pod zaostřením. Vzorkem použitým pro záznam těchto snímků funkce rozptylu bodu byla fluorescenční kulička o průměru 0,1 mikrometru umístěná v glycerolu (index lomu 1,47), přičemž imerzní oleje měly indexy lomu uvedené na obrázku.

Důležitým aspektem je, jak funkce rozptylu bodu ovlivňuje tvorbu obrazu v mikroskopu. Teoretický model tvorby obrazu považuje funkci bodového rozptylu za základní jednotku obrazu. Jinými slovy, funkce rozprostření bodu je pro obraz tím, čím je cihla pro dům. Nejlepším obrazem, který kdy může být, je sestava funkcí bodového rozptylu a zvýšení zvětšení tuto skutečnost nezmění. Jak vysvětluje známá učebnice teoretické optiky (Born a Wolf: Principles of Optics): „Zvýšením výkonu okuláru nelze zvýraznit detaily, které nejsou přítomny v primárním obraze, protože každý prvek primárního obrazu je malý difrakční obrazec a skutečný obraz, jak jej vidíme v okuláru, je pouze souborem zvětšených obrazů těchto obrazců.“

Jako příklad uvažujme populaci fluorescenčních kuliček s nižším rozlišením vložených mezi krycí sklíčko a sklíčko mikroskopu. Zaostřený obraz tohoto vzorku odhalí oblak teček, což je ve skutečnosti disk obklopený malým souborem prstenců (v podstatě Airyho disk; viz obrázek 4(a)). Pokud tento vzorek mírně rozostříme, objeví se v místě, kde se na zaostřeném snímku nacházely jednotlivé tečky, větší sada soustředných kroužků (obrázek 4b). Když se pořídí trojrozměrný obraz tohoto vzorku, pak se pro každou kuličku zaznamená kompletní funkce rozprostření bodu. Funkce bodového rozptylu popisuje, co se stane s každým bodovým zdrojem světla poté, co projde zobrazovacím systémem.

Právě popsaný proces rozostření je matematicky modelován jako konvoluce. Operace konvoluce popisuje aplikaci funkce bodového rozptylu na každý bod ve vzorku: světlo vyzařované z každého bodu v objektu je konvolvováno s funkcí bodového rozptylu, čímž vznikne výsledný obraz. Tato konvoluce bohužel způsobuje, že se body ve vzorku stávají rozmazanými oblastmi v obraze. Jas každého bodu v obraze je pomocí konvoluční operace lineárně vztažen k fluorescenci každého bodu ve vzorku. Protože funkce bodového rozptylu je trojrozměrná, rozmazání z funkce bodového rozptylu je ze své podstaty trojrozměrný jev. Obraz z libovolné ohniskové roviny obsahuje rozmazané světlo z bodů nacházejících se v této rovině smíšené s rozmazaným světlem z bodů pocházejících z jiných ohniskových rovin.

Situaci lze shrnout myšlenkou, že obraz je tvořen konvolucí vzorku s funkcí rozprostření bodu. Dekonvoluce tento proces obrací a pokouší se rekonstruovat vzorek z rozmazaného obrazu.

Aberace ve funkci rozptylu bodu

Funkci rozptylu bodu lze definovat buď teoreticky s využitím matematického modelu difrakce, nebo empiricky pořízením trojrozměrného obrazu fluorescenční kuličky (viz obrázek 3). Teoretická funkce bodového rozptylu má obecně axiální a radiální symetrii. Ve skutečnosti je funkce bodového rozptylu symetrická nad a pod rovinou x-y (axiální symetrie) a rotačně kolem osy z (radiální symetrie). Empirická funkce bodového rozptylu se může výrazně odchýlit od dokonalé symetrie (jak je znázorněno na obrázku 3). Tato odchylka, častěji označovaná jako aberace, vzniká v důsledku nepravidelností nebo chybného nastavení kterékoli součásti optické soustavy zobrazovacího systému, zejména objektivu, ale může se vyskytnout i u jiných součástí, jako jsou zrcadla, rozdělovače svazku, tubusové čočky, filtry, clony a apertury. Čím kvalitnější jsou optické součásti a čím lépe je mikroskop seřízen, tím více se empirická funkce rozptylu bodu blíží svému ideálnímu symetrickému tvaru. Konfokální i dekonvoluční mikroskopie závisí na tom, aby se funkce rozptylu bodu co nejvíce blížila ideálnímu případu.

Nejčastější aberací, se kterou se setkáváme v optické mikroskopii a kterou dobře zná každý zkušený a profesionální mikroskopista, je sférická aberace. Projevem této aberace je axiální asymetrie tvaru funkce rozprostření bodu s odpovídajícím zvětšením, zejména podél osy z (obr. 3). Výsledkem je značná ztráta rozlišení a intenzity signálu. V praxi je typickým zdrojem sférické aberace nesoulad mezi indexy lomu imerzního média přední čočky objektivu a montážního média, v němž je vzorek ponořen. Na důležitost minimalizace této aberace je třeba klást obrovský důraz. Ačkoli dekonvoluce může částečně obnovit ztracené rozlišení, žádné zpracování obrazu nemůže obnovit ztracený signál.