Bilineare Filterung & Bilineare Interpolation

Schauen Sie sich das folgende Bild an. Kannst du die Werte an den Punkten A, B und C berechnen?

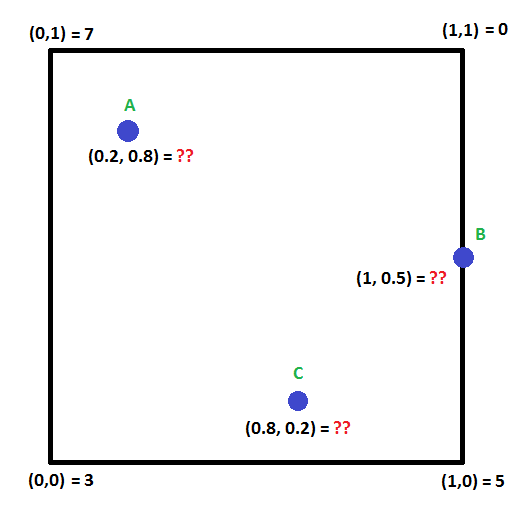
Dafür gibt es eine Technik, die man bilineare Interpolation nennt und die die Idee der linearen Interpolation auf zwei Dimensionen erweitert.

Um die bilineare Interpolation zu berechnen, führt man einfach eine lineare Interpolation auf einer Achse und dann auf der anderen durch.

Schauen Sie sich diese Beispiele an:

Punkt A
Punkt A hat eine Koordinate von (0.2,0.8). Beginnen wir mit der X-Achse.

Zunächst werden wir eine Interpolation über den oberen Rand des Quadrats auf der X-Achse durchführen. Das bedeutet, dass wir 0,2 (20%) des Weges von 7 nach 0 gehen müssen. Diese 0,2 ist unsere X-Achsenkoordinate. Um das zu berechnen, gehen wir folgendermaßen vor:
7 + (0-7) * 0,2 = 5,6

Als Nächstes führen wir eine Interpolation über den unteren Teil des Quadrats auf der X-Achse durch. Ähnlich wie oben gehen wir also 0,2 (20%) des Weges von 3 bis 5. Um das zu berechnen, gehen wir folgendermaßen vor:
3 + (5-3) * 0,2 = 3,4

Nachdem wir nun über unsere X-Achse interpoliert haben, müssen wir über unsere Y-Achse interpolieren. Wir gehen nun 0,8 (80 %) des Weges von unserem unteren Wert (dem Wert von Y = 0) zu unserem oberen Wert (dem Wert von Y = 1). Der untere Wert ist der untere Interpolationswert (3,4) und der obere Wert ist der obere Interpolationswert (5,6).

Wir müssen also 0,8 (80%) des Weges von 3,4 nach 5,6 gehen. Um das zu berechnen, gehen wir folgendermaßen vor:
3,4 + (5,6 – 3,4) * 0,8 = 5,16

Der Wert am Punkt A ist also 5,16. Das folgende Bild soll helfen, den Prozess, den wir durchlaufen haben, visuell zu erklären.

Punkt B

Punkt B hat die Koordinaten (1.0,0.5).

Beginnen wir wieder mit der Interpolation der X-Achse (obwohl man leicht mit der Y-Achse beginnen könnte, wenn man wollte! Man käme zum gleichen Ergebnis).

Bei der Interpolation der X-Achse über die Oberseite müssen wir 1,0 (100 %) des Weges von 7 bis 0 gehen. Sie können sich sicher denken, wie die Antwort lautet, aber hier ist sie berechnet:
7 + (0-7) * 1,0 = 0

Gleichermaßen können wir die Interpolation der X-Achse über die Unterseite durchführen. Wir müssen 1,0 (100%) des Weges von 3 bis 5 gehen.
3 + (5-3) * 1,0 = 5

Als nächstes kommt die Interpolation der Y-Achse. Wir müssen 0,5 (50%) des Weges von 5 nach 0 gehen.
5 + (0-5) * 0,5 = 2,5

So, der Wert am Punkt B ist 2,5. Das sollte auch Sinn machen, wenn man sich das Diagramm ansieht. Es ist im Grunde 1d lineare Interpolation zwischen 5 und 0 und liegt auf halbem Weg dazwischen, so dass die Antwort 2,5 intuitiv Sinn machen sollte.

Punkt C

Punkt C hat eine Koordinate von (0,8,0,2).

Noch einmal, lassen Sie uns die Interpolation der X-Achse über die Oberseite der Box durchführen. Wir müssen 0,8 (80%) des Weges von 7 bis 0 gehen.
7 + (0-7) * 0,8 = 1,4

Dann müssen wir die X-Achsen-Interpolation über den unteren Teil des Kastens durchführen. Wir müssen 0,8 (80%) des Weges von 3 bis 5 gehen.
3 + (5-3) * 0,8 = 4,6

Zuletzt noch die Interpolation der y-Achse. Wir müssen 0,2 (20%) von 4,6 auf 1,4 gehen.
4,6 + (1,4-4,6) * 0,2 = 3,96

Der Wert von Punkt C ist 3.96

Bilineare Filterung

Während die bilineare Interpolation nützlich ist, wenn man ein Gitter von Daten hat, innerhalb dessen man Werte interpolieren möchte (wie z.B. ein Höhenfeld, das das Gelände darstellt?!), ist sie in der Spieleentwicklung vor allem bei der bilinearen Texturfilterung von Vorteil.

Grundsätzlich wird bei einer Texturkoordinate, die nicht perfekt mit der Mitte eines Pixels in der Textur übereinstimmt (weil es einen Rest gibt), der Bruchteil der Koordinate innerhalb dieses Pixels verwendet, um eine bilineare Interpolation zwischen den 4 beteiligten Pixeln durchzuführen, um die endgültige Pixelfarbe zu erhalten. Die bilineare Interpolation wird für jeden der Kanäle durchgeführt: Rot, Grün, Blau und Alpha.

Das Endergebnis ist ziemlich gut! Schauen Sie sich das Bild unten an, um es in Aktion auf einer Textur zu sehen, die wir zu weit herangezoomt sind. Auf der linken Seite wird die bilineare Filterung verwendet, während auf der rechten Seite nur das nächstgelegene Pixel angezeigt wird.

Die bilineare Texturfilterung muss vier Pixel lesen, um zwischen ihnen interpolieren zu können, anstatt nur ein einziges Pixel zu lesen, wie es beim Nearest Pixel Sampling der Fall ist. Mehr Pixel-Reads = mehr Overhead und nicht so billig (rechnerisch) zu verwenden.

Links

Für einige Leute, die das hier lesen, ist diese Information ziemlich grundlegend und sie fragen sich vielleicht, warum ich mir die Mühe gemacht habe, darüber zu schreiben. Im nächsten Beitrag finden Sie etwas ziemlich Bizarres über bilineare Filterung. Das war als Sprungbrett für die nächste Sache nötig, die ich euch zeigen möchte 😛

Wikipedia: Lineare Interpolation

Wikipedia: Bilineare Interpolation

Wikipedia: Bilineare Filterung

Die dunkle Seite der bilinearen Filterung

Schauen Sie sich diese Links an, um mehr über die Unzulänglichkeiten (und einige Umgehungen) des hardwarebasierten bilinearen Samplings zu erfahren:
iq: Hardware-Interpolation
iq: Verbesserte Textur-Interpolation