9.5 – Identifizierung einflussreicher Datenpunkte

In diesem Abschnitt lernen wir die folgenden beiden Maße zur Identifizierung einflussreicher Datenpunkte kennen:

• Difference in Fits (DFFITS)
• Cook’s Distances

Der Grundgedanke hinter jedem dieser Maße ist derselbe, nämlich die Beobachtungen einzeln zu löschen und jedes Mal das Regressionsmodell mit den verbleibenden n-1 Beobachtungen neu anzupassen. Anschließend werden die Ergebnisse unter Verwendung aller n Beobachtungen mit den Ergebnissen verglichen, bei denen die i-te Beobachtung gelöscht wurde, um festzustellen, wie viel Einfluss die Beobachtung auf die Analyse hat. Auf diese Weise können wir die potenziellen Auswirkungen jedes Datenpunkts auf die Regressionsanalyse bewerten.

Differenz der Anpassungen (DFFITS)

Die Differenz der Anpassungen für die Beobachtung i, bezeichnet als DFFITSi, ist wie folgt definiert:

\

Wie Sie sehen, misst der Zähler die Differenz der vorhergesagten Antworten, die sich ergeben, wenn der i-te Datenpunkt in die Analyse einbezogen bzw. ausgeschlossen wird. Der Nenner ist die geschätzte Standardabweichung der Differenz der vorhergesagten Antworten. Daher quantifiziert die Differenz der Anpassungen die Anzahl der Standardabweichungen, um die sich der angepasste Wert ändert, wenn der i-te Datenpunkt weggelassen wird.

Eine Beobachtung gilt als einflussreich, wenn der absolute Wert ihres DFFITS-Wertes größer ist als:

\

wobei, wie immer, n = die Anzahl der Beobachtungen und k = die Anzahl der Prädiktorterme (d. h. die Anzahl der Regressionsparameter ohne den Achsenabschnitt). Es ist wichtig zu beachten, dass es sich hierbei nicht um eine feste Regel handelt, sondern nur um einen Richtwert! Es ist nicht schwer, verschiedene Autoren zu finden, die einen leicht abweichenden Leitfaden verwenden. Daher bevorzuge ich oft eine viel subjektivere Richtlinie, z. B. dass ein Datenpunkt als einflussreich gilt, wenn der absolute Wert seines DFFITS-Wertes wie ein wunder Daumen aus den anderen DFFITS-Werten heraussticht. Natürlich handelt es sich hierbei um ein qualitatives Urteil, und das ist auch gut so, denn Ausreißer sind naturgemäß subjektive Größen.

Beispiel #2 (wieder). Schauen wir uns den Unterschied in der Anpassungsmessung für diesen Datensatz an (influence2.txt):

Wenn wir y auf x regressieren und die Differenz der Anpassungen abfragen, erhalten wir die folgende Softwareausgabe:

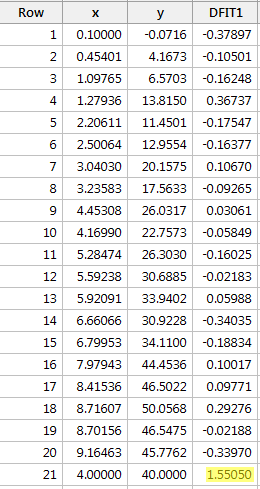
Nach der oben definierten objektiven Richtlinie betrachten wir einen Datenpunkt als einflussreich, wenn der Absolutwert seines DFFITS-Wertes größer ist als:

\

Nur ein Datenpunkt – der rote – hat einen DFFITS-Wert, dessen Absolutwert (1.55050) größer als 0,82 ist. Auf der Grundlage dieser Richtlinie würden wir daher den roten Datenpunkt als einflussreich betrachten.

Beispiel #3 (erneut). Schauen wir uns den Unterschied im Anpassungsmaß für diesen Datensatz an (influence3.txt):

Wenn wir y auf x regressieren und die Differenz der Anpassungen abfragen, erhalten wir die folgende Softwareausgabe:

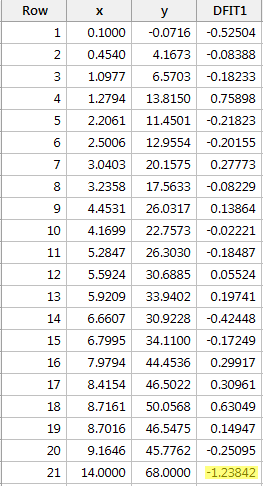
Nach der oben definierten objektiven Richtlinie betrachten wir einen Datenpunkt als einflussreich, wenn der Absolutwert seines DFFITS-Wertes größer ist als:

\

Nur ein Datenpunkt – der rote – hat einen DFFITS-Wert, dessen Absolutwert (1.23841) größer als 0,82 ist. Daher würden wir, basierend auf dieser Richtlinie, den roten Datenpunkt als einflussreich betrachten.

Als wir diesen Datensatz zu Beginn dieser Lektion untersuchten, kamen wir zu dem Schluss, dass der rote Datenpunkt die Regressionsanalyse nicht sonderlich beeinflusst. In diesem Fall deutet der Unterschied in den Anpassungsmaßen jedoch darauf hin, dass er tatsächlich einen Einfluss hat. Was ist hier los? Letztendlich geht es darum, zu erkennen, dass alle in dieser Lektion vorgestellten Messgrößen nur Hilfsmittel sind, die den Datenanalysten auf potenziell einflussreiche Datenpunkte hinweisen. Letztendlich sollte der Analytiker den Datensatz zweimal analysieren – einmal mit und einmal ohne die markierten Datenpunkte. Wenn die Datenpunkte das Ergebnis der Regressionsanalyse signifikant verändern, sollte der Forscher die Ergebnisse beider Analysen angeben.

Wenn wir in diesem Beispiel die eher subjektive Richtlinie verwenden, ob der absolute Wert des DFFITS-Wertes wie ein wunder Daumen heraussticht, werden wir den roten Datenpunkt wahrscheinlich nicht als einflussreich einstufen. Denn der nächstgrößere DFFITS-Wert (in absoluten Zahlen) ist 0,75898. Dieser DFFITS-Wert unterscheidet sich nicht allzu sehr von dem DFFITS-Wert unseres „einflussreichen“ Datenpunktes.

Beispiel #4 (wieder). Schauen wir uns den Unterschied in der Anpassungsmessung für diesen Datensatz an (influence4.txt):

Wenn wir y gegen x regressieren und die Differenz der Anpassungen abfragen, erhalten wir die folgende Softwareausgabe:

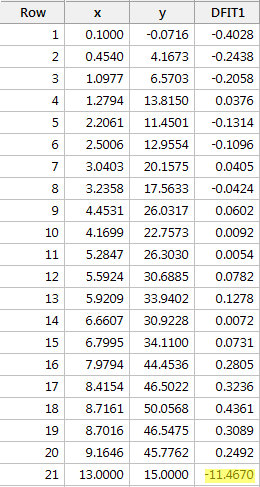
Unter Verwendung der oben definierten objektiven Richtlinie betrachten wir einen Datenpunkt als einflussreich, wenn der absolute Wert seines DFFITS-Wertes größer ist als:

\

Was denken Sie? Sticht einer der DFFITS-Werte wie ein böser Daumen hervor? Errr – der DFFITS-Wert des roten Datenpunktes (-11,4670 ) ist sicherlich von einer anderen Größenordnung als alle anderen. In diesem Fall sollte es wenig Zweifel daran geben, dass der rote Datenpunkt einflussreich ist!

Cook’s Distance

Das Cook’sche Abstandsmaß, das mit Di bezeichnet wird, ist wie folgt definiert:

\.\]

Es sieht ein wenig unübersichtlich aus, aber das Wichtigste ist, dass Cook’s Di sowohl vom Residuum ei (im ersten Term) als auch von der Hebelwirkung hii (im zweiten Term) abhängt. Das heißt, sowohl der x-Wert als auch der y-Wert des Datenpunktes spielen bei der Berechnung von Cooks Distanz eine Rolle.

Kurz gesagt:

• Di fasst direkt zusammen, wie sehr sich alle angepassten Werte ändern, wenn die i-te Beobachtung gelöscht wird.
• Ein Datenpunkt mit einem großen Di zeigt an, dass der Datenpunkt die angepassten Werte stark beeinflusst.

Lassen Sie uns untersuchen, was genau diese erste Aussage im Zusammenhang mit einigen unserer Beispiele bedeutet.

Beispiel 1 (erneut). Sie erinnern sich vielleicht, dass die Darstellung dieser Daten (influence1.txt) darauf hindeutet, dass es für dieses Beispiel weder Ausreißer noch einflussreiche Datenpunkte gibt:

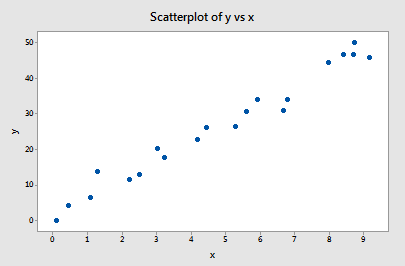
Wenn wir y auf x unter Verwendung aller n = 20 Datenpunkte regressieren, stellen wir fest, dass der geschätzte Abschnittskoeffizient b0 = 1,732 und der geschätzte Steigungskoeffizient b1 = 5,117. Entfernt man den ersten Datenpunkt aus dem Datensatz und regressiert y auf x mit den verbleibenden n = 19 Datenpunkten, so ergibt sich der geschätzte Abschnittskoeffizient b0 = 1,732 und der geschätzte Steigungskoeffizient b1 = 5,1169. Wie erhofft und erwartet, ändern sich die Schätzungen nicht allzu sehr, wenn der eine Datenpunkt entfernt wird. Wenn man diesen Prozess fortsetzt, indem man jeden Datenpunkt einzeln entfernt und die daraus resultierenden geschätzten Steigungen (b1) gegen die geschätzten Achsenabschnitte (b0) aufträgt, erhält man:

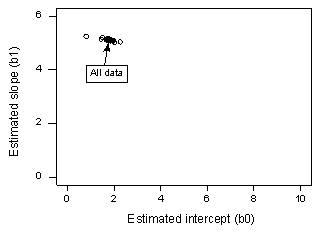
Der durchgehende schwarze Punkt stellt die geschätzten Koeffizienten auf der Grundlage aller n = 20 Datenpunkte dar. Die offenen Kreise stellen die geschätzten Koeffizienten dar, die sich ergeben, wenn jeder Datenpunkt einzeln gelöscht wird. Wie Sie sehen können, sind die geschätzten Koeffizienten alle gebündelt, unabhängig davon, welcher Datenpunkt, wenn überhaupt, entfernt wird. Dies deutet darauf hin, dass kein Datenpunkt die geschätzte Regressionsfunktion und damit auch die angepassten Werte übermäßig beeinflusst. In diesem Fall würden wir erwarten, dass alle Cook’schen Abstandsmaße, Di, klein sind.

Beispiel #4 (wieder). Sie erinnern sich vielleicht, dass die Darstellung dieser Daten (influence4.txt) darauf hindeutet, dass ein Datenpunkt einflussreich und ein Ausreißer für dieses Beispiel ist:

Wenn wir y auf x unter Verwendung aller n = 21 Datenpunkte regressieren, stellen wir fest, dass der geschätzte Abschnittskoeffizient b0 = 8,51 und der geschätzte Steigungskoeffizient b1 = 3,32. Entfernt man den roten Datenpunkt aus dem Datensatz und regressiert y auf x mit den verbleibenden n = 20 Datenpunkten, so ergibt sich der geschätzte Abschnittskoeffizient b0 = 1,732 und der geschätzte Steigungskoeffizient b1 = 5,1169. Wow – die Schätzungen ändern sich erheblich, wenn ein Datenpunkt entfernt wird. Wenn man diesen Prozess fortsetzt, indem man jeden Datenpunkt einzeln entfernt und die sich daraus ergebenden geschätzten Steigungen (b1) gegen die geschätzten Achsenabschnitte (b0) aufträgt, erhält man:

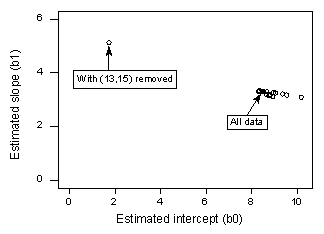
Auch hier stellt der durchgehende schwarze Punkt die geschätzten Koeffizienten auf der Grundlage aller n = 21 Datenpunkte dar. Die offenen Kreise stellen die geschätzten Koeffizienten dar, die sich ergeben, wenn jeder Datenpunkt einzeln gelöscht wird. Wie Sie sehen können, sind die geschätzten Koeffizienten mit Ausnahme des roten Datenpunktes (x = 13, y = 15) alle gebündelt, unabhängig davon, welcher Datenpunkt entfernt wird. Dies deutet darauf hin, dass der rote Datenpunkt der einzige Datenpunkt ist, der die geschätzte Regressionsfunktion und damit auch die angepassten Werte übermäßig beeinflusst. In diesem Fall würden wir erwarten, dass das Cook’sche Abstandsmaß Di für den roten Datenpunkt groß und das Cook’sche Abstandsmaß Di für die übrigen Datenpunkte klein ist.

Verwendung von Cook’schen Abstandsmaßen. Das Schöne an den obigen Beispielen ist die Möglichkeit, mit einfachen Diagrammen zu erkennen, was vor sich geht. Leider können wir uns im Falle der multiplen Regression nicht auf einfache Diagramme verlassen. Stattdessen müssen wir uns auf Richtlinien verlassen, um zu entscheiden, wann ein Cook’sches Abstandsmaß groß genug ist, um einen Datenpunkt als einflussreich zu behandeln.

Hier sind die Richtlinien, die üblicherweise verwendet werden:

• Wenn Di größer als 0,5 ist, dann ist der i-te Datenpunkt einer weiteren Untersuchung wert, da er einflussreich sein könnte.
• Wenn Di größer als 1 ist, dann ist der i-te Datenpunkt sehr wahrscheinlich einflussreich.
• Oder, wenn Di wie ein wunder Daumen aus den anderen Di-Werten heraussticht, ist er mit ziemlicher Sicherheit einflussreich.

Beispiel #2 (wieder). Schauen wir uns das Cook’sche Abstandsmaß für diesen Datensatz an (influence2.txt):

Bei der Regression von y auf x und der Abfrage der Cook’schen Abstandsmaße erhalten wir die folgende Softwareausgabe:

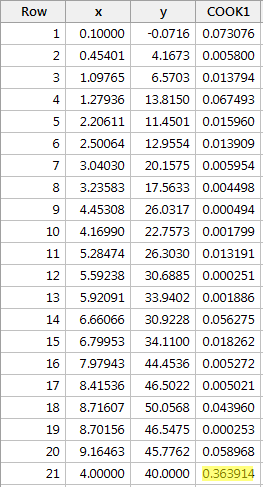
Das Cook’sche Abstandsmaß für den roten Datenpunkt (0,363914) sticht im Vergleich zu den anderen Cook’schen Abstandsmaßen ein wenig hervor. Dennoch ist das Cook’sche Abstandsmaß für den roten Datenpunkt kleiner als 0,5. Auf der Grundlage des Cook’schen Abstandsmaßes würden wir den roten Datenpunkt daher nicht als einflussreich einstufen.

Beispiel #3 (erneut). Schauen wir uns das Cook’sche Abstandsmaß für diesen Datensatz an (influence3.txt):

Bei der Regression von y auf x und der Abfrage der Cook’schen Abstandsmaße erhalten wir die folgende Softwareausgabe:

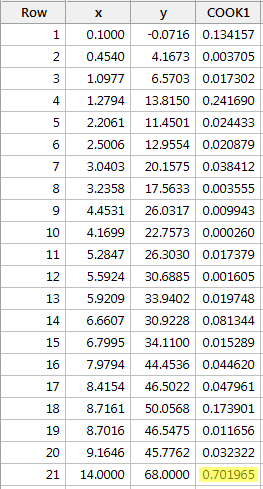
Das Cook’sche Abstandsmaß für den roten Datenpunkt (0,701965) sticht im Vergleich zu den anderen Cook’schen Abstandsmaßen etwas hervor. Dennoch ist das Cook’sche Abstandsmaß für den roten Datenpunkt größer als 0,5, aber kleiner als 1. Daher würden wir auf der Grundlage des Cook’schen Abstandsmaßes vielleicht weitere Untersuchungen durchführen, aber den roten Datenpunkt nicht unbedingt als einflussreich einstufen.

Beispiel #4 (erneut). Schauen wir uns das Cook’sche Abstandsmaß für diesen Datensatz (influence4.txt) an:

Wenn wir y auf x regressieren und die Cook’schen Abstandsmaße abfragen, erhalten wir die folgende Softwareausgabe:

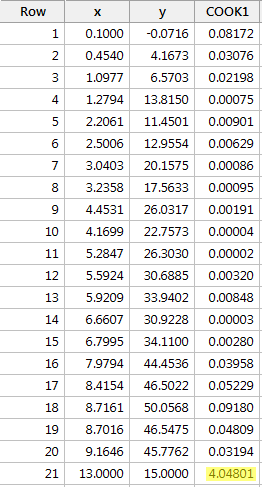
In diesem Fall sticht das Cook’sche Abstandsmaß für den roten Datenpunkt (4.04801) im Vergleich zu den anderen Cook’schen Abstandsmaßen deutlich hervor. Außerdem ist das Cook’sche Distanzmaß für den roten Datenpunkt größer als 1. Daher würden wir den roten Datenpunkt auf der Grundlage des Cook’schen Distanzmaßes – nicht überraschend – als einflussreich einstufen.

Eine alternative Methode zur Interpretation der Cook’schen Distanz, die manchmal verwendet wird, besteht darin, das Maß mit der F(k+1, n-k-1)-Verteilung in Beziehung zu setzen und den entsprechenden Perzentilwert zu ermitteln. Wenn dieses Perzentil weniger als 10 oder 20 Prozent beträgt, dann hat der Fall nur einen geringen Einfluss auf die angepassten Werte. Liegt er dagegen bei 50 Prozent oder sogar darüber, hat der Fall einen großen Einfluss. (Alles, was „dazwischen“ liegt, ist eher zweideutig.)